Composite Corrugated Core

Sandwich structures have been used over a long time applications where the weight of the member is critical, such as packaging, civil, naval, automotive and aerospace industries due to their low mass to stiffness ratio and high impact absorption capacity. Some instances of their applications in daily life are cardboard sandwich cores used for packaging, metal corrugated roofs, hulks, automotive chassis and bumpers, fuselage and morphing wing. In nature, where mechanical design required to be optimized, sandwich structures are used such as the human skull which is made up of two layers of dense compact bone separated by a "core" of lower density material.

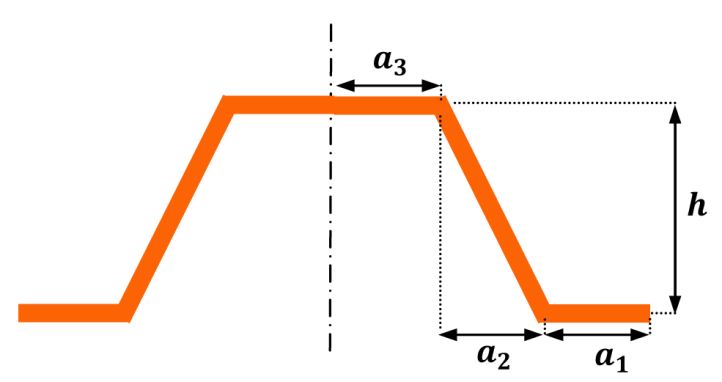
A branch of sandwich structures is the composite corrugated panels consisting of two sheets called liners, which are partitioned by a trapezoidal wave shaped fluted core referred to as medium. Figure 1 depicts the composite corrugated core made of woven Glass fibers.

(a)	(b)
Fig. 1 The composite corrugated core and corresponded sketch of the unit cell

These panels have exceedingly anisotropic behavior. They are stiff and flexible along and transverse to the corrugation direction, respectively. Composite corrugated panels have been proposed as a candidate for application in morphing wings. This is due to the fact that wing structures must be stiff so as to withstand bending due to aerodynamic forces, and flexible so as to match the most efficient form in a flight regime.

For the designed composite corrugated core as a candidate of morphing wing, the tensile and bending deformation in the three-dimensional space is a concern for its significant influence on the aerodynamic performance of the morphing aircraft. Therefore, one of the goals of this paper is to investigate the mechanical behavior of composite corrugated core as a member of sandwich panel.

To do so, trapezoidal corrugated panels made of prepreg glass fiber were manufactured using aluminium molds.

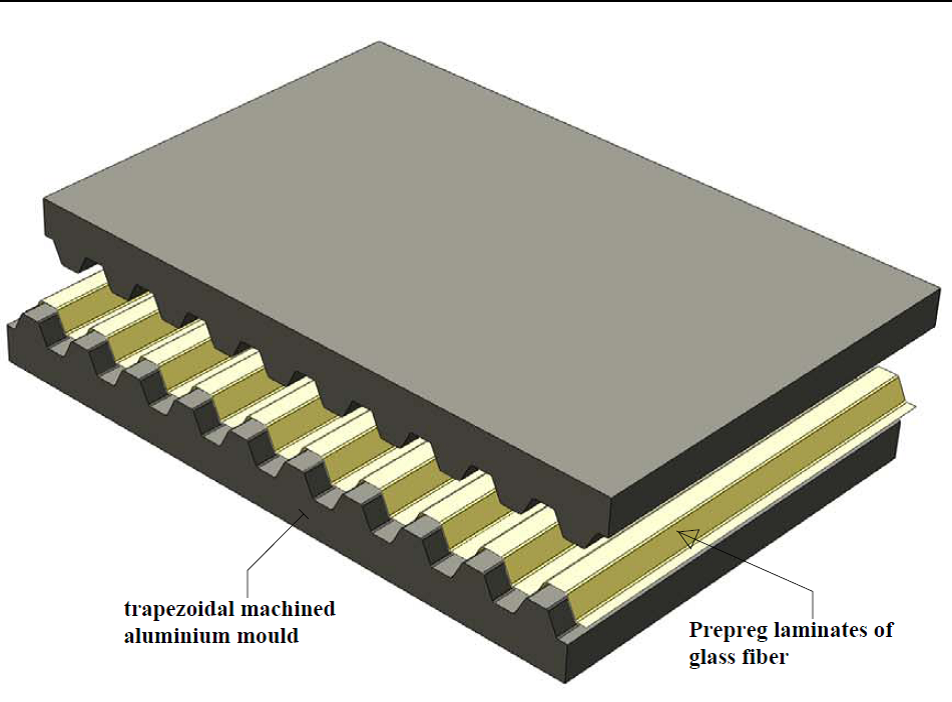Fig. 2 Schematic of trapezoidal machined aluminium mould and Prepreg laminates of glass fiber

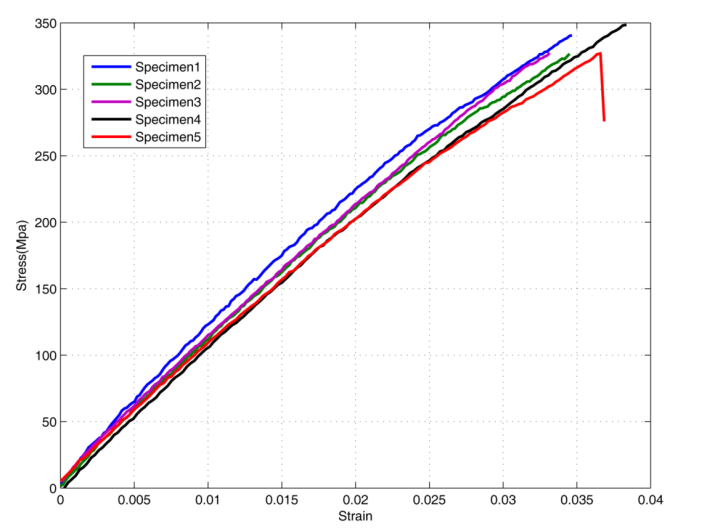
The mechanical properties of the material were first determined using simple tension tests on standard samples (Figure 3).

(a)	(b)
Fig. 3 Specimens prepared for tensile test and corresponded stress-strain curves inuniaxial tensile tests

The panels were then subjected to tensile and three-point bending tests and the force-displacement curve for each case was recorded (Figure 4 and 5).

Fig. 4 Testing machine and composite corrugated core during three points bending test

Fig. 5 Microscopic images of delamination in trapezoidal corrugated specimen region during tensile testing

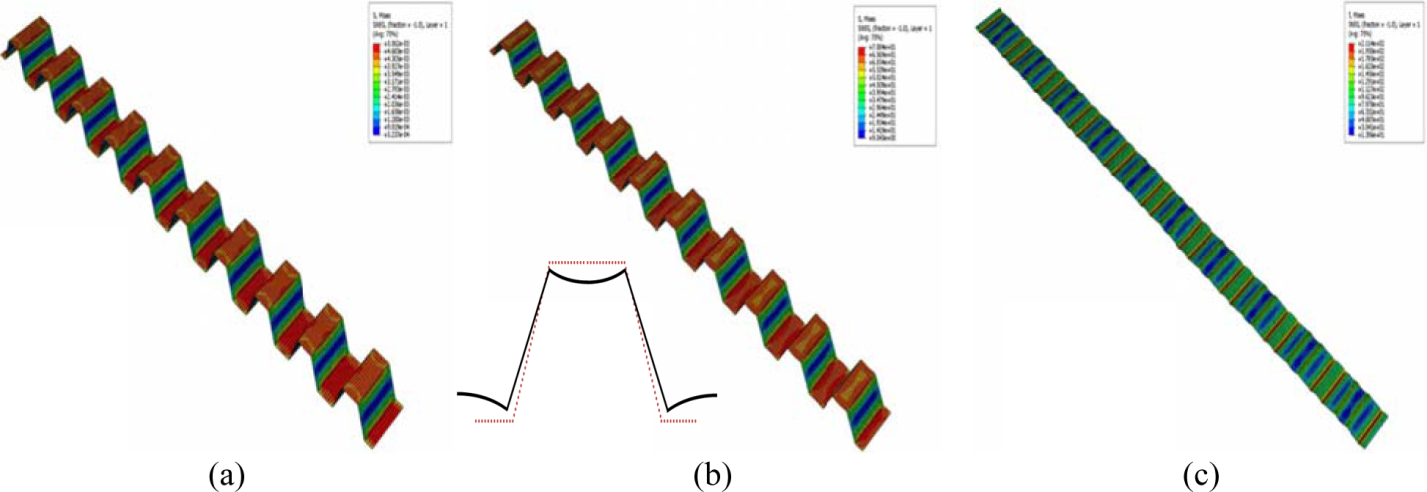
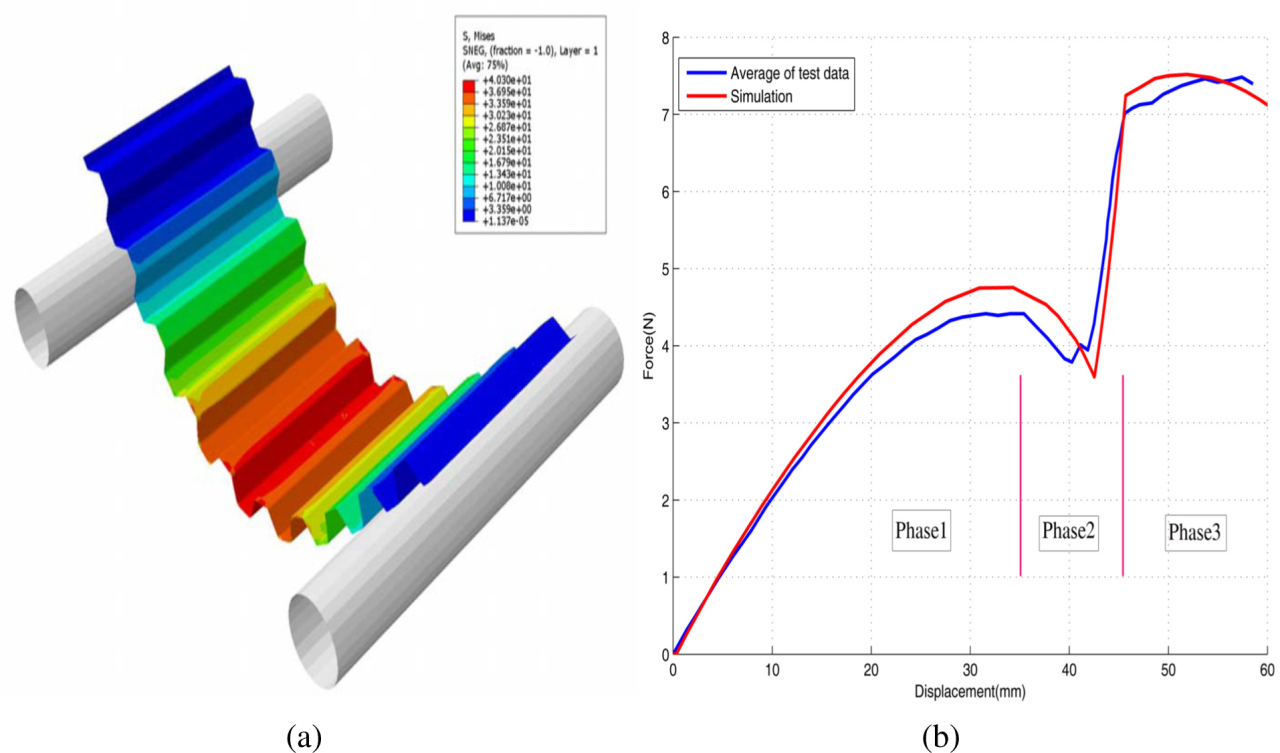
Next, a finite element model of the panel was constructed and used to predict the behavior of the panels under tension and three-point bending (Figure 6 and 7).

Fig. 6 Three different phases of corrugated core in tensile test

Fig. 7 Simulation of corrugated core in three points bending test and comparison of force-displacement behavior from experiment and simulation

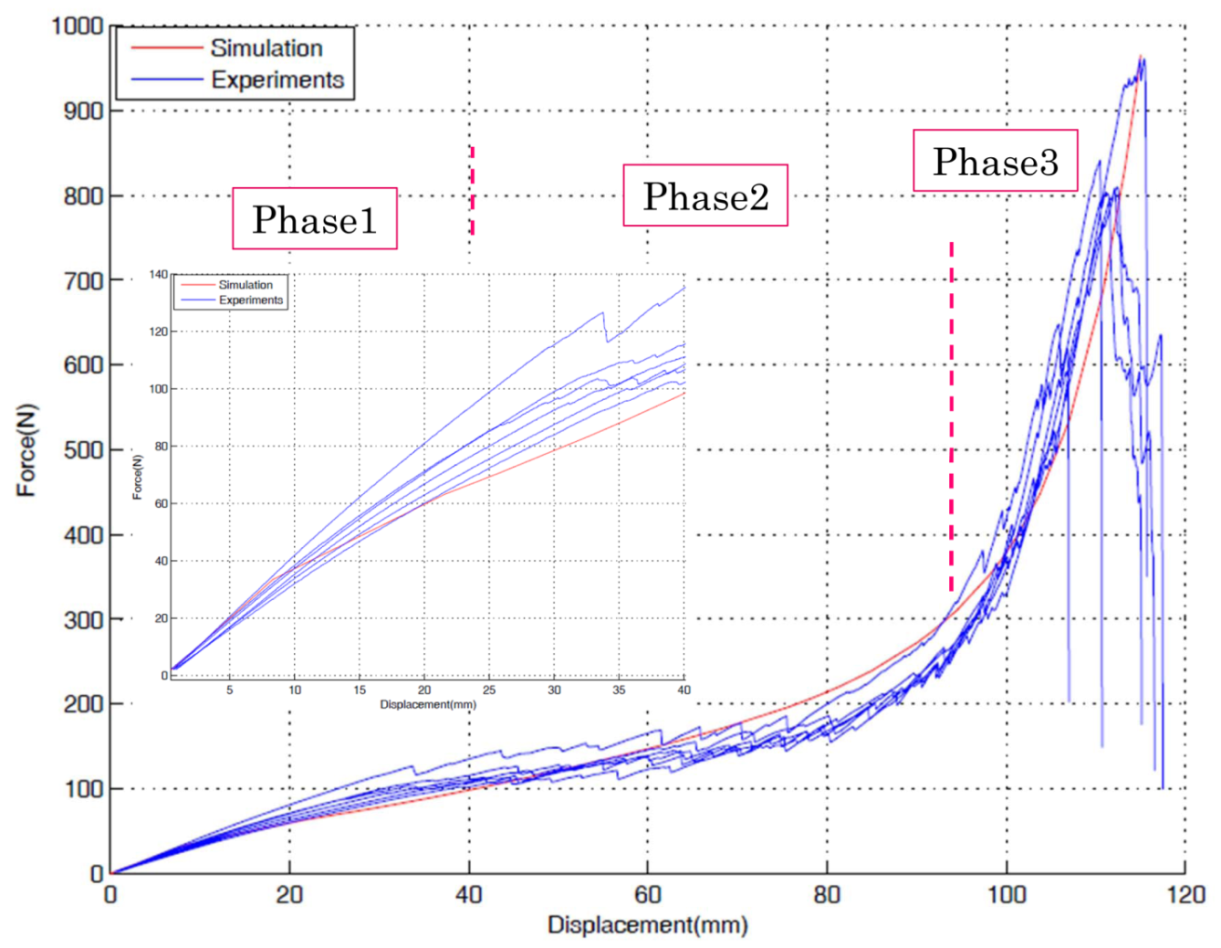
Finally, analytical solutions for linear part of the force-displacement curves were proposed and used to estimate the mechanical characteristics of the panel (Figure 8).

Fig. 8 Comparison of force-displacement behavior in tension (experiment and simulation)

A good degree of correlation illustrated the suitability of the finite element method for modeling the mechanical behavior of corrugated laminate panels in both tension and bending. The results also indicate that the panels exhibit extreme anisotropic stiffness properties which may be useful in aircraft morphing wing skin applications.